快速傅里叶变换

你一定在某些地方听说过FFT的大名。

快速傅里叶变换 (Fast Fourier Transform) 在计算机科学中相关重要。我们用它来做信号处理，图像压缩，大整数乘法等等，并且最重要的是，它是算法设计中将数学性质和算法结构完美结合的典中典。

上一届学到的Strassen矩阵乘法用了巧妙的数学构造优化了复杂的$O(n^3)$。FFT也是一样。多项式乘法（也就是卷积）最直观的算法是$O(n^2)$，为了打破这个平静，我们必须使用分治策略。

但FFT比归并或者Strassen更进一步：它不只是简单的却分数组，还引入了复数域的数学性质来配合分治。

多项式乘法的表示

首先我们要明白我们在解决什么问题。我们想要尝试解决的问题是多项式乘法，或者更广义地说，两个序列的卷积。

例如我们在这里有一个多项式：

$$A(x) = a_0 + a_1x + \dots + a_{n-1}x^{n-1}$$

可以用 系数表示法 来定义。就比如一个向量 $[a_0, a_1, ...]$ 。

如果你想要算出两个多项式$A(x)$ 和 $B(x)$ 的乘积 $C(x) = A(x) \cdot B(x)$，你会发现这个过程非常麻烦。
由于每一项 $a_{i}x^{i}$ 都需要和 $b_{j}x^{j}$ 相乘，结果会贡献到 $x^{i + j}$这一项上。这就是卷积。如果你暴力求职，那么你需要对这些系数两层循环，复杂度来到了 $O(n^2)$，慢的要死。

但实际上除了系数表示法，我们还可以使用 点值表示法 来确定多项式。一个 $n - 1$ 次的多项式，可以被 $n$ 个不同的点唯一确认。这就好比两点确定一条直线，三点确定一条抛物线一样：

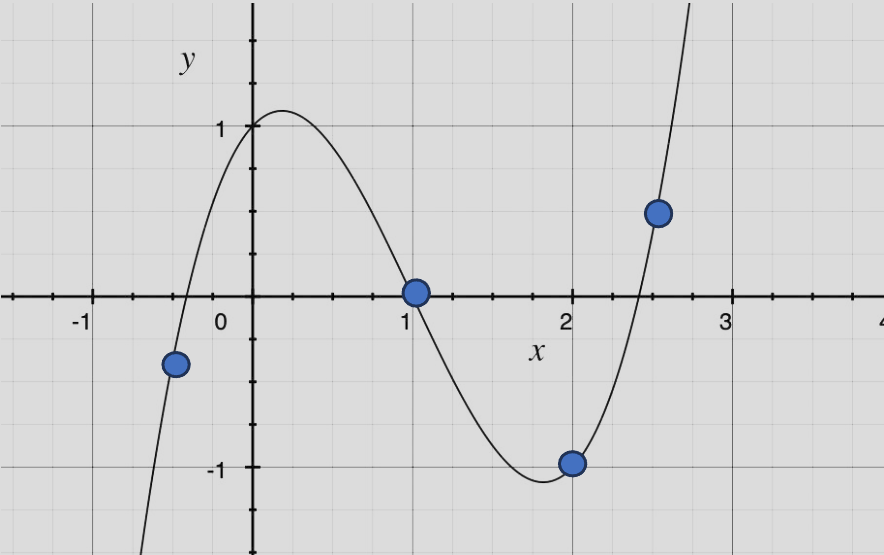
$$p(x) = 1 + x - 3x^2 + x^3$$

这里我们知道可以对多项式AB来进行采样：

$A$ : $(x_0, y_a0)$, $(x_1, y_a1)$
$B$ : $(x_0, y_b0)$, $(x_1, y_b1)$

这时候如果我们想要求得多项式乘积的值将会非常简单。因为 $C(x) = A(x) \cdot B(x)$，所以你只需要将对应 $y$ 值乘起来即可：$y_c0 = y_a0 \cdot y_b0$，相同的$x$坐标值的$y$值乘起来。

那么我们该如何采样？要计算$C(x) = A(x) \times B(x)$，我们必须保证$A$和$B$实在同一组x坐标上进行采样的。因此，我们的操作流程是：

选取一组公共的$x$点集：$x_0, x_1, ..., x_k$
算出$A$在这些点的值：$y_{a0}, y_{a1}, ...$
同理，算出$B$的值：$y_{b0}, y_{b1}, ...$
最后能够得出这些点在C的值必然是 $(x_0, y_{a0} \cdot y_{b0}), (x_1, y_{a1} \cdot y_{b1})$。

如此，我们只需要遍历一遍数组即可。复杂度来到 $O(n)$。

你有没有想过万一我指定了$n$个点值，但是结果对应了两个不同的多项式怎么办？或者找不到任意多项式该咋办？你如何证明点值表示法一定能够使用点值来确定唯一的一个多项式？

设一个次数小于$n$的多项式：

$$A(x) = a_0 + a_{1}x + a_{2}x^2 + ... + a_{n-1}x^{n-1}$$

我们要找多项式的系数 $a_0, a_1, ..., a_{n-1}$，如果我们知道$n$个点$(x_0, y_0), ..., (x_{n-1}, y_{n-1})$，我们可以列出$n$个方程：

$$a_0 + a_1x_0 + \dots + a_{n-1}x_0^{n-1} = y_0$$ $$...$$ $$a_0 + a_1x_{n-1} + \dots + a_{n-1}x_{n-1}^{n-1} = y_{n-1}$$

把这个方程组写成矩阵形式：

$$\begin{bmatrix}
1 & x_0 & x_0^2 & \dots & x_0^{n-1} \\
1 & x_1 & x_1^2 & \dots & x_1^{n-1} \\
\vdots & \vdots & \vdots & \ddots & \vdots \\
1 & x_{n-1} & x_{n-1}^2 & \dots & x_{n-1}^{n-1}
\end{bmatrix} \cdot \begin{bmatrix}
a_0 \\ a_1 \\ \vdots \\ a_{n-1}
\end{bmatrix} = \begin{bmatrix}
y_0 \\ y_1 \\ \vdots \\ y_{n-1}
\end{bmatrix}$$

中间那个充满了 $x$ 的矩阵就是 Vandermonde 矩阵。

只要 $x_0, \dots, x_{n-1}$ 这些点互不相同，Vandermonde 矩阵的行列式就不为 0，也就是矩阵可逆。
这意味着对于任意一组给定的$y$值，方程组有且仅有唯一解。这从数学上保证了点值表示法是稳健的。

我们直到该如何选点了，也确定点值表示法非常稳健，那么选点数量有没有要求？

如果你有两个$n-1$次多项式相乘，结果$C(x)$的次数会来到$2(n-1)$，也就是接近$2n$次。要唯一确定一个$2n$次的多项式，我们需要$2n$个点，而不是$n$个点。说得好，但是为什么呢？

由于多项式$A(x)$和$B(x)$的最高次数都是$n - 1$。它们的乘积$C(x) = A(x) \cdot B(x)$，最高次数来到了$(n - 1) + (n - 1) = 2n - 2$，由于第一项是0次，所以$C(x)$一共有$2n-1$个系数。
要唯一确定一个系数为$2n - 1$的多项式，我们至少需要$2n - 1$个点。

所以我们在选点的时候，虽然$A$和$B$本身只需要$n$个点就能够确定，但是为了给结果$C(x)$留足空间，我们需要在一开始就选取$2n$个点，或者更多。

在算法实现里为了方便，一般我们会凑成2的幂次数量来选点。

以上就是FFT的核心思想了。由于我们使用点值处理乘法这么快，我们的策略是：

求值：将多项式从抽象的系数提炼成点值
点乘：将点值花$O(n)$的时间算出结果点值
插值/逆变换：由于点值表示法是可逆的，所以我们将得出的结果点值转化回系数。

但是如果我们随机选取 $n$个点，好比说 $x_0, ..., x_{n-1}$，带入多项式求值。

你需要计算$n$次，每次耗时$O(n)$。为什么？假设我们要计算一个多项式在点$k$的取值：

$$P(k) = a_0 + a_1k + a_2k^2 + ... + a_{n-1}k^{n-1}$$

如果点是普通整数，例如1, 2, 3，那么每一项$k^j$都需要单独进行计算。计算$k^j$的代价是$O(j)$，整个多项式在一个点上的计算代价就是$O(n)$。要把这$n$个点全部计算出来，就是 $O(n^2)$

所以到头来我们这一圈还没有解决根本问题，最后的复杂度还是$O(n^2)$。

FFT要做的是找到一种极快的方法，来完成这个传送过程。我们不能随便选点，相反，我们需要有策略地选取点值。

单位根

这一部分我们主要解决选点问题。

FFT的巧妙之处就在于选择单位根。单位根的模长始终是1，所以无论指数多大，数值大小都不会爆炸。例如，$\omega_{n}^{j} = e^{2\pi k/n}$，不管$j$多大，结构总是单位圆上的一个点，大小始终是1。这就避免了数值溢出和精度问题。

同时，单位根的对称性能够让我们把计算拆分成一半一半，从而把复杂度降到$O(n \log{n})$

我们想象复数平面上的单位圆。在这个圆上的任何一个点，无论你怎么做乘法，结果仍然会在这个圆上。
我们需要在这个圆上均匀的切$n$刀。这些切点就叫$n$次单位根。也就是满足$\omega^{n} = 1$的复数$\omega$。就像一个时钟。如果$n = 4$，那么这四个点就分别在3, 12, 9, 6点钟位置。

我们定位 主单位根 (Principal Root of Unity) $\omega_{n}$ 为逆时针方向的第一个刻度：

$$\omega_n = e^{i \frac{2\pi}{n}} = \cos(\frac{2\pi}{n}) + i\sin(\frac{2\pi}{n})$$

如果你不熟悉欧拉公式 $e^{ix}$，只需要把它想象成一个旋转操作：$\omega_n$代表旋转$1/n$圈。

那么我们就知道这$n$个点实际上就是$\omega_n$的幂：$\omega_n^0, \omega_n^1, \omega_n^2, \dots, \omega_n^{n-1}$。

单位根有一个关键性质：$\omega_n^{n/2} = -1, \quad \omega_n^{n/4} = i$，这些对称性意味着我们可以把多项式的计算拆成两半再合并。这让分治法成为可能。我们可以先把规模减半，递归计算，然后使用单位根的对称性快速合并。

如果选择普通点，这种对称性就不复存在，分治就没办法使用，复杂度就一直停留在$O(n^2)$。

折半引理

为什么选这些点就能够使用分治法？

如果想要在这些点上使用分治，那么这些点就可以在拆分后，从规模为$n$的多项式拆成两个规模为$n/2$的子问题。换句话说，这就要求我们选的这$n$个点，在平方之后能够变成$n/2$个点。

这里就很明显了，由于我们使用了复数，以$n=8$为例，我们需要计算多项式在八个点上的值：

$${\omega_8^0, \omega_8^1, \omega_8^2, \omega_8^3, \omega_8^4, \omega_8^5, \omega_8^6, \omega_8^7}$$

如果将所有的点平方，你会发现：

$\omega_8^0$ (0度) 平方 $\to$ $\omega_8^0$ (0度)
$\omega_8^1$ (45度) 平方 $\to$ $\omega_8^2$ (90度)
...
$\omega_8^4$ (180度) 平方 $\to$ $\omega_8^8$ (360度 = 0度) (与第一点重合)
$\omega_8^5$ (225度) 平方 $\to$ $\omega_8^{10} = \omega_8^2$ (90度) (与第二点重合)

以此类推，我们会发现这$n$个单位根进行平方操作后就变成了$n/2$个点，因为有一半的数值回合现有的点值重合。这$n/2$个新点，就刚好是$n/2$次单位根。

$$(\omega_n^k)^2 = \omega_{n/2}^k$$

这意味着我们在顶层有 $n$ 个输入点。进入下一子问题层时，我们只需要处理 $n/2$ 个点。

FFT的前向算法

有了这个性质，我们就可以真正开始构建算法了。

首先，我们要分。

我们要计算$A(x)$在$n$个单位根上的值。我们不能像归并排序那样把数组左边和右边切开，实际上，我们需要按照下标的奇偶性来切分：

假设原始的多项式是：

$$A(x) = a_{0} + a_{1}x + a_{2}x^2 + ... + a_{n}x^n$$

我们可以把系数分成两组，分别是：

$a_0 + a_{2}x^2 + a_{4}x^4 + ...$ 是偶数下标
$a_{1}x + a_{3}x^3 + a_{5}x^5 + ...$ 是奇数下标

我们希望把这两部分都写成某个多项式在$x^2$上的形式，于是这里我们定义：

$$A_{\text{even}}(z) = a_0 + a_{2}z + a_{4}z^2 + ...$$
$$A_{\text{odd}}(z) = a_1 + a_{3}z + a_{5}z^2 + ...$$

观察上方的规律，我们可以得到偶数部分可以用 $A_{\text{even}}(x^2)$ 表示，同理，奇数部分可以用 $x \cdot A_{\text{odd}}(x^2)$ 表示。

因此，合并原来的多项式就是：

$$A(x) = A_{\text{even}}(x^2) + x \cdot A_{\text{odd}}(x^2)$$

接下来我们递归调用FFT，分别计算：

$A_{\text{even}}(x)$ 在 $n/2$个点 ${\omega_{n/2}^0, ..., \omega_{n/2}^{n/2-1}}$上的值
$A_{\text{odd}}(x)$ 在 $n/2$个点 ${\omega_{n/2}^0, ..., \omega_{n/2}^{n/2-1}}$上的值

怎么来的？由于我们已经知道：

$$A(x) = A_{\text{even}}(x^2) + x \cdot A_{\text{odd}}(x^2)$$

所以如果我们要计算 $A(\omega_{n}^k)$，就变成了：

$$A(\omega_{n}^k) = A_{\text{even}}((\omega_{n}^k)^2) + \omega_{n}^k \cdot A_{odd}((\omega_{n}^k)^2)$$

由于：

$$(\omega_{n}^k)^2 = \omega_{n}^{2k} = \omega_{n/2}^k$$

这说明当我们在$n$个单位根上计算$A(x)$时，实际上只需要在$n/2$个单位根上计算 $A_{even}(x)$ 和 $A_{odd}(x)$即可。

分治完毕后我们要合并。我们拿到了两个子问题的结果数组，就把他们叫 $y_{\text{even}}$ 和 $y_{\text{odd}}$ 吧。我们要把它们拼回 $n$ 个结果。

结果公式可以从上面的公式推导出来，就是：

$$A(\omega_{n}^k) = A_{\text{even}}(\omega_{n}^{2k}) + \omega_{n}^k \cdot A_{\text{odd}}(\omega_{n}^{2k})$$

利用性质 $\omega_{n}^{2k} = \omega_{n/2}^k$，我们可以知道对于从0到 $n/2 - 1$的$k$来说：

前半部分的结果就是：

$$y_k = y_{\text{even}}[k] + \omega_{n}^k \cdot y_{\text{odd}}[k]$$

而后半部分的结果就是：

$$y_{k + n/2} = y_{\text{even}}[k] - \omega_{n}^k \cdot y_{\text{odd}}[k]$$

这就是大名鼎鼎的蝴蝶操作。

蝴蝶操作

那么你很迷惑这些公式是什么意思，前半部分和后半部分到底是什么东西。
蝴蝶操作的前后半公式往往难以理解。首先我们在前面推导出了最基本的拆分公式：

$$P(x) = P_{\text{even}}(x^2) + x \cdot P_{\text{odd}}(x^2)$$

这个公式告诉我们，如果你想算出多项式$P$在点$x$的值，你只需要算出两个小多项式$P_{\text{even}}$和$P_{\text{odd}}$在$x^2$点的值，然后代入公式计算即可。

而在FFT中我们要计算的是$P$在$n$个单位根上的值： $\omega_{n}^0, \omega_{n}^1, ..., \omega_{n}^{n - 1}$

我们把这些$n$个点分成两组。

前半组是 $k = 0$ 到 $n/2 - 1$。如果$n = 8$，那么$k = 0, 1, 2, 3$
那么后半组就是 $k = n/2$ 到 $n - 1$。在上面的例子中就是$k = 4, 5, 6, 7$

先来看前半组的推导。如果我们要计算第 $k$个点的值，我们就把$x = \omega_{n}^k$带入核心公式：

$$P(\omega_n^k) = P_{even}((\omega_n^k)^2) + \omega_n^k \cdot P_{odd}((\omega_n^k)^2)$$

利用折半引理 $\omega_{n}^{2k} = \omega_{n/2}^k$：

$$P(\omega_n^k) = P_{even}(\omega_{n/2}^k) + \omega_n^k \cdot P_{odd}(\omega_{n/2}^k)$$

其中，$P_{\text{even}}(\omega_{n/2}^k)$就是我们递归调用FFT(even)返回的结果数组中的第$k$个元素，我们记作$y_{even}[k]$。同理，$P_{\text{odd}}(\omega_{n/2}^k)$就是调用FFT(odd)中的第$k$个元素，记作$y_{\text{odd}}[k]$。

前半部分的公式就变成了：

$$y[k] = y_{\text{even}}[k] + \omega_{n}^k \cdot y_{\text{odd}}[k]$$

前半部分还算比较简单，后半部分的推导就比较令人迷惑了。

后半部分的点，可以写成$k' = k + n/2$，其中$k$还是从0到$n/2 - 1$。比如$n = 8$，第四个点就是$0 + 4$，第五个点就是$1 + 4$。

因此，在整理索引后，我们把 $x = \omega_{n}^{k + n/2}$ 带入核心公式：

$$P(\omega_n^{k+n/2}) = P_{even}((\omega_n^{k+n/2})^2) + \omega_n^{k+n/2} \cdot P_{odd}((\omega_n^{k+n/2})^2)$$

首先来看看平方部分。我们需要计算$(\omega_{n}^{k + n/2})^2$：

$$(\omega_{n}^{k+n/2})^2 = \omega_{n}^{2k+n} = \omega_n^{2k} \cdot \omega_{n}^n$$

由于$\omega_n^n = 1$，转了一圈回到原点，因此：

$$= \omega_n^{2k} \cdot 1 = \omega_{n/2}^{k}$$

你发现后半部分输入值的平方与前半部分输入值的平方是一模一样的。这意味着$P_{even}$和$P_{odd}$不需要重新计算，我们只需要复用前半部分拿到的$y_{even}[k]$和$y_{odd}[k]$就可以了。

然后来看看编号的系数部分 $x = \omega_{n}^{k + n/2}$：

$$\omega_{n}^{k + n/2} = \omega_{n}^k \cdot \omega_{n}^{n/2}$$

由于$\omega_n$是把圆切成$n$份，$\omega_n^{n/2}$就是切了$n/2$份，也就是转了180度。
在复平面上，转180°就是等于乘以-1，因此：

$$\omega_n^{k + n/2} = -\omega_n^k$$

最后，我们把上面两点结合起来，带回原式：

$$P(\omega_n^{k+n/2}) = P_{even}(\dots) + (-\omega_n^k) \cdot P_{odd}(\dots)$$
$$y[k + n/2] = y_{even}[k] - \omega_n^k \cdot y_{odd}[k]$$

OK了。这里的蝴蝶操作就是利用了复数的对称性来化简计算。前半个圆上面的点$k$结果是$A + \omega^k B$，后半个是$A - \omega^k B$。这里的 $A(y_{even}[k])$ 和 $B(y_{odd}[k])$ 对于这两个点是完全共用的，区别就在于中间的加号变成了减号。

FFT逆变换

如果说前向FFT就是把稀疏表示转换成点值表示，那么逆变换的作用就是把这个过程反过来。

通过计算前向FFT，我们得到了一个长度为$n$的序列在$n$个单位根上的取值。而逆向FFT要做的是输入单位根的取值，来输出原始的多项式系数。

换句话说，逆向FFT就是把取值重新组合，恢复原始信号或系数。我们在点值界完成了乘法，现在手中拿着$n$个点值$y_0, y_1, ..., y_{n-1}$。我们的目标是求出系数向量 $a = [a_0, a_1, ..., a_{n-1}]$

回顾一下前向变换，我们做的事本质上就是一个矩阵乘法：

$$y = V \cdot a$$

$y_0, y_1, ..., y_{n-1}$合并写成一个向量$y$，输入系数 $a_0, a_1, ..., a_{n-1}$写成向量$a$。其中V就是充满了$\omega$的范德蒙德矩阵。如果我们要求出$a$，只需要将范德蒙德矩阵移到等式左边：

$$a = V^{-1} \cdot y$$

所以，逆变换的问题等价于，我们求矩阵$V$的逆矩阵$V^{-1}$长什么样？

还记得范德蒙德矩阵吗？

原矩阵$V$中的元素是$\omega_{n}^{jk}$，而它的逆矩阵$V^{-1}$里面的元素都是 $\frac{1}{n} \omega_{n}^{-jk}$。唯二区别在于：

指数里的$\omega$全部变成了$\omega^{-1}$
所有的元素多除了一个 $n$。

所以实际上要计算 $V^{-1}$，我们不需要使用高斯消元法这种$O(n^3)$的算法就行了。直接套用这个规律就可以了！

如此，逆向FFT的步骤就是：

直接调用刚才的FFT函数
由于逆矩阵的变化非常简单，这时候我们只需要把单位根参数从$\omega_n$换成$\omega_{n}^{-1}$。在复平面上，$\omega_n^{-1} = e^{-i2{\pi}/n}，相当于角度取负$
最后，拿到FFT返回的结果数组后，我们将里面的每一个数字都除以$n$。

完整流程

到此，我们已经完成了对于整个FFT过程的全部讲解。我们来总结一下吧。

如果我们要计算$C(x) = A(x) \times B(x)$，假设$A$与$B$的次数都是$n-1$。我们会经过下列流程：

准备

结果$C$的次数是$2n - 2$。我们要把$A$与$B$的系数数组补$0$，补到长度为$N$为止。
$N$是大于$2n - 2$的2的幂次，比如说$2n$。

求值

y_a = FFT(A, N, ω)
y_b = FFT(B, N, ω)

这一步我们耗时 $2 \times O(N\log N)$。

点乘

y_c = [ y_a[0]*y_b[0], ..., y_a[N-1]*y_b[N-1] ]
这一步耗时$O(N)$。

插值取逆

coeffs_c = FFT(y_c, N, ω^-1)
然后我们将coeffs_c中的每一个数字除以$N$。
这一步耗时$O(N\log N)$。

总复杂度就是：

$$O(N\log N) + O(N) + O(N\log N) = \mathbf{O(N\log N)}$$

相当于暴力的$O(N^2)$，当$N$的值非常大时，这个算法快不少。这就是为什么现在我们能够在计算机上快速处理音频，图像以及大数据计算的原因。