上一章我们通过聚类发现了数据的"分组"结构。今天我们来解决另一个无监督学习的难题:维度灾难。
想象你有一张100x100的图片,它就是10000维空间里的一个点。处理这么高维的数据不仅慢,而且容易过拟合(记得Ch6的VC维吗?维度越高,模型越复杂)。
能不能把这10000维的数据"压缩"成50维,同时还不丢失主要信息?这就是PCA (主成分分析) 要做的事。
PCA是一个从直觉到数学推导都比较有挑战性的硬骨头。它不仅涉及线性代数(特征值、特征向量),还涉及优化的思想。
线性代数
为了能理解PCA,我们需要使用到基础的线性代数知识。我们不把线性代数当作枯燥的计算规则,而是把它当作描述高维空间的语言。
在 PCA 中,我们要在高维空间(比如 1000 维)里旋转、投影、寻找“主轴”,没有这套工具是不行的。
下面应该都是老朋友了。如果bro的线性代数学的很不错,那你直接跳过这一块就可以。
向量 (Vector)
我们通常把一个数据样本$x$看作一个列向量,维度为$d(x \in \mathbb{R}^d)$。
向量是$d$维空间中的一个点,或者是从原点指向该点的一个箭头。
矩阵 (Matrix)
有一个矩阵$A$。$A$不仅仅只是一张数字表,它代表了一种线性变换 (Linear Transformation)。
当你用矩阵$A$乘以一个向量$x$时($Ax$),我们实际上对空间中的$x$进行了扭曲。这个向量可能发生了旋转,拉伸,或者剪切。具体看$A$的内容。
矩阵乘法 (Matrix Multiplication)
$C = AB$,这代表变换的叠加。先做$B$变换,然后再做$A$变换。
执行矩阵乘法之前需要做一步维度检查。简而言之:
$$(m \times n) \times (n \times p) \rightarrow (m \times p)$$
其中,中间的$n$必须匹配,否则两个矩阵无法相乘。而且,$AB \ne BA$。
投影的几何
既然我们已经了解了最基础的现代内容,我们就可以开始理解什么是投影了。
首先我们可以知道向量内积 (或者点乘积 / Dot Product) 可以通过该公式算得:
$$x^Ty = \sum(x_i y_i) = ||x|| ||y|| cos(\theta)$$
如果$x^Ty = 0$,那么证明这两个向量夹角为90°,两个向量垂直。
向量自己的内积是该向量长度的平方,$x^Tx = ||x||^2$。
那么PCA的核心动作:投影 (Projection) 是怎样的呢?想象我们有一个单位向量$u$:它的长度为一,仅用来代表一个方向,那么向量$x$在$u$方向上的投影长度是多少?
$$x^Tu$$
由于PCA的目的就是找到一个方向$u$,使得所有数据点$x_i$投影到$u$上之后,分布的最散,也就是方差最大。因此你会在后面反复看见$x^Tu$。
特征值与特征向量
如果说矩阵$A$是一个空间变换器,那么特征向量就是它的骨架。
对于方阵$A$,如果存在非零向量$v$和标量$\lambda$,使得:
$$Av = \lambda v$$
我们就称$v$是特征向量 (Eigenvector),$\lambda$则是特征值 (Eigenvalue)。
通常情况下,矩阵$A$乘以一个向量$x$,会改变$x$的方向和长度。但是对于特征向量$v$来说,矩阵$A$作用在它上面只会改变它的长度,不会改变它的方向。这些$v$指示了矩阵变换的“主轴方向”。
后面我们会发现,数据的协方差矩阵$S$描述了数据的分布形状,通常来说它看起来像一个橄榄球。这个橄榄球的长轴方向,就是$S$的最大特征向量。长轴的长度是方差大小,就刚好对应了最大特征值$\lambda$。这就是为什么PCA最终是一个求得特征值的问题。
PCA如何降维打击
想象你有一张大小为$100 \times 100$ 的灰度图片。如果每一个像素是一个特征,那么数据的原始维度就是$d = 10000$维。
你发现这10000个像素之间存在大量冗余。如果背景是全黑色的,那么这几千个像素其实只需要用一个“背景为黑”的信息就能概括。因此我们要做的就是找到一个更低维度的$r$,例如$r = 50$,来尝试只用50个数就能概括这张图的主要特征。
最大方差
那么你就想:怎么样概括数据来降维才算好?PCA的逻辑是:保留差异。
假设我们有一堆数据点,分布为一个椭圆形状。我们想要把它们投影到一条直线上,从2D降维到1D。我们可以选择两个方案来达成这一点:
随便画一条线,然后尝试将数据点投影到这条线上。你会发现投影后的挤在一起,糊在一团。这不是很好,因为很多原本不同的点,经过投影之后变得更难区分了。这就是我们之前说的投影后方差小的概念:
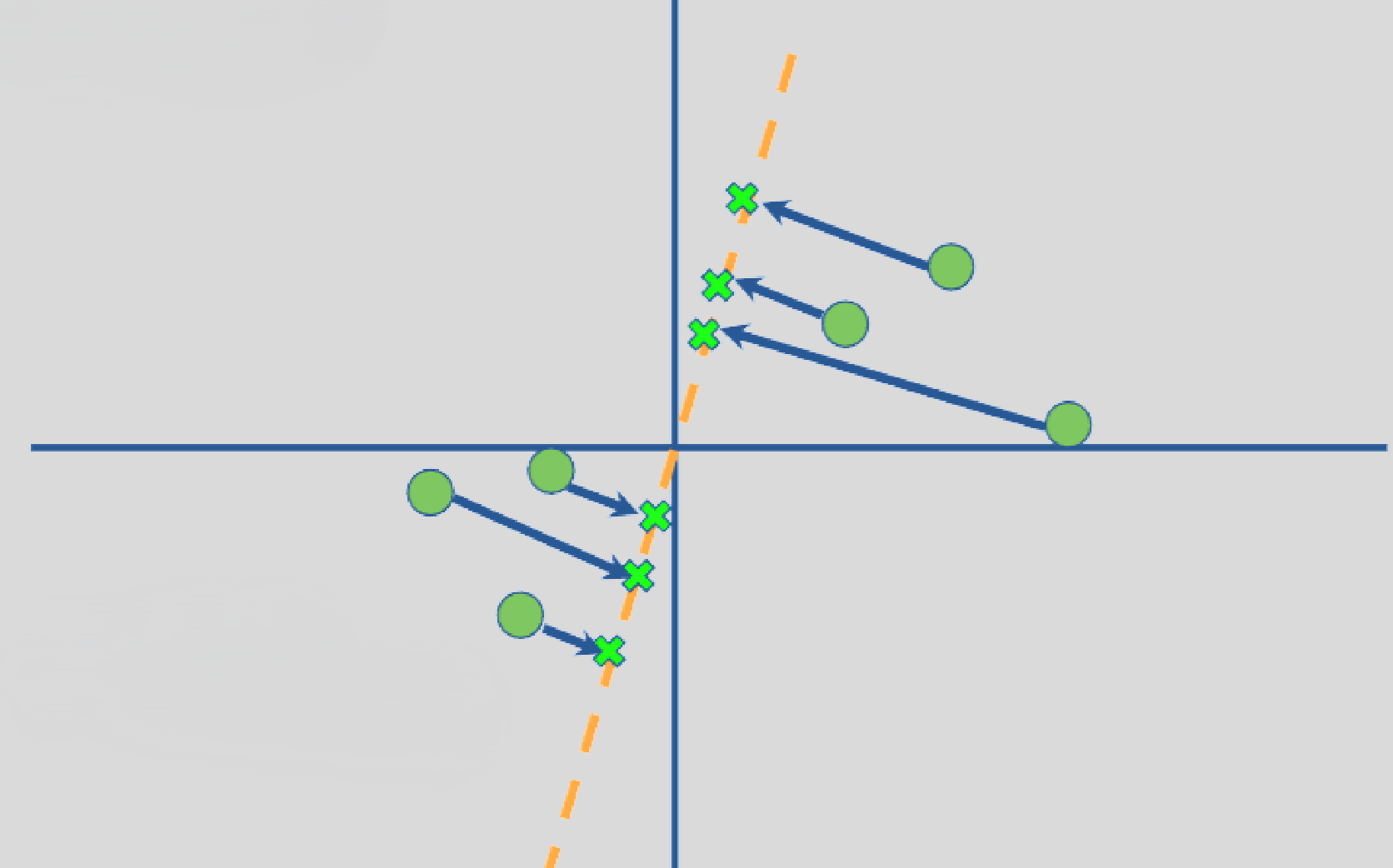
我们沿着数据“椭圆”的长轴画一条线。这样你发现投影之后的点拉的很开,分布很广。这才是我们想要的投影效果,因为这样的投影方式保留了数据组内部最大的差异。这就是刚才提到的,PCA的目标是达到投影后数据方差大的根本逻辑:
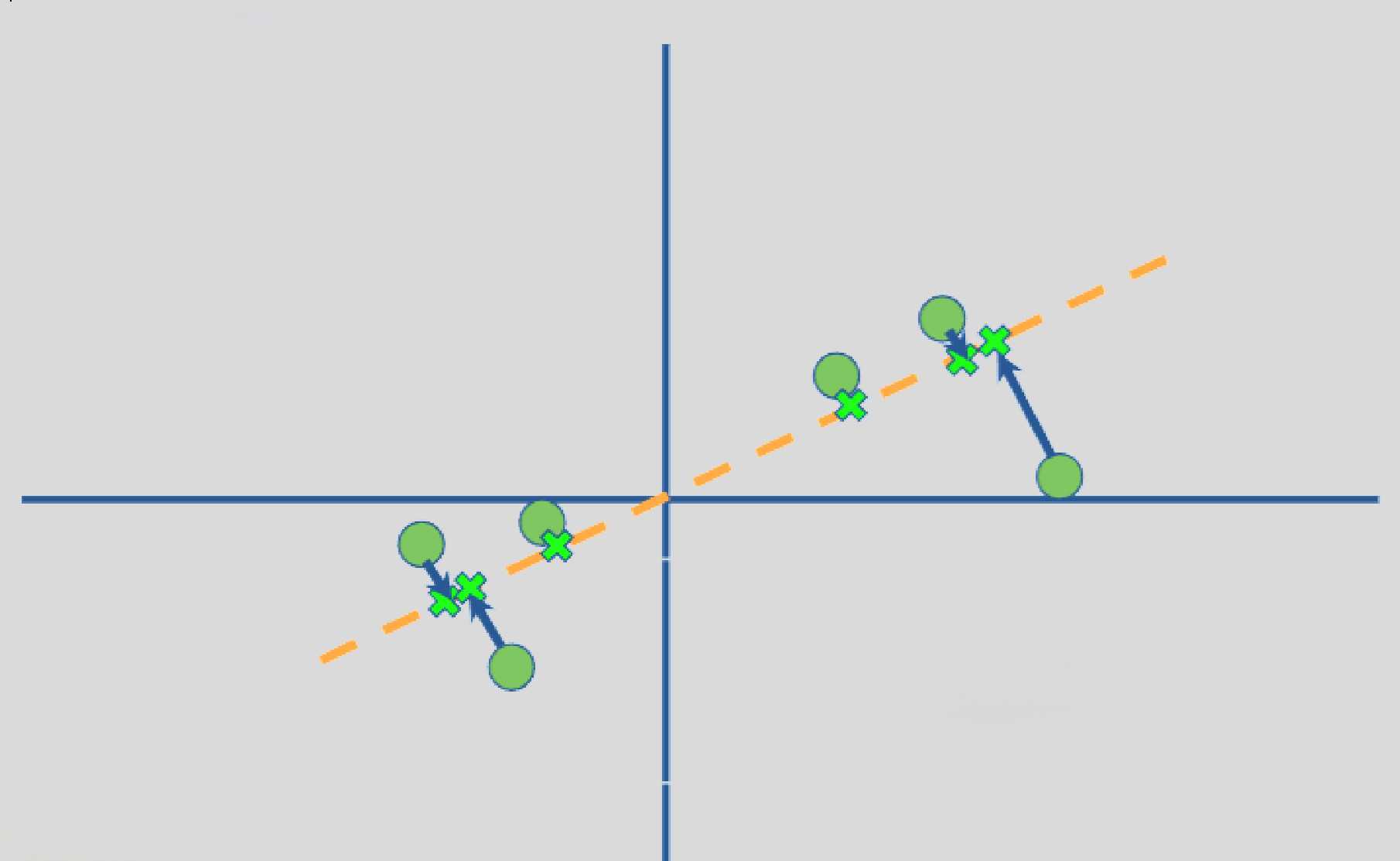
我们的目标就是寻找一个方向$u$,使得数据投影到$u$上后的方差最大。这个方向$u$就叫第一主成分 (Principal Component 1)
想象你手里拿着一根法棍。这根法棍存在于三维空间,而你要做的是把它拍扁成一张照片。这就是降维。那么为了让照片里的法棍看起来最清楚(保留最多信息/方差最大),你应该朝着哪个角度拍?你要找到法棍的长轴,这就是PCA的直觉。
预处理:中心化
在做PCA之前,我们需要先做一部预处理。首先是减去均值:
$$New x_i = x_i - \mu$$
这样一来,所有数据的中心就被挪到了原点。我们之所以这样做是为了方便计算方差:
我们知道方差公式为$Var = \frac{1}{n} \sum(val_i - mean)^2$。如果已经中心化了,那么mean=0,方差公式即可直接简化掉$mean$项。这简化了我们后续的推导。
翻译目标函数
接下来我们可以进行数据投影了。
我们输入中心化后的数据$x_1, ..., x_n$,将每个$x_i$投影到单位向量$u$上,而$u$就是我们要找的长轴方向,且$u^Tu = 1$。由投影公式可得,该点的投影值就应该是$z_i = {x_i}^Tu$。
我们关心投影后的方差。由于输入的均值是0,则投影后的均值也是0。这就是为什么我们要输入均值为0的数据。那么方差就是投影值平方和的平均:
$$Var= \frac{1}{n-1} \sum_{i-1}^n (z_i)^2 = \frac{1}{n-1} \sum_{i=1}^n ({x_i}^Tu)^2$$
处于性能考虑,我们当然想要把求和变成矩阵乘法。如何做到呢?这是线性代数最美妙的瞬间之一:
还记得$z_i = {x_i}^Tu$是一个标量吗?标量的平方实际上可以写成$a^2 = a \cdot a = a^Ta$:
$$ (x_i^T u)^2 = (x_i^T u) (x_i^T u) = (u^T x_i) (x_i^T u) = u^T (x_i x_i^T) u $$
把求和符号放进去:
$$ \text{Var} = \frac{1}{n-1} \sum_{i=1}^n u^T (x_i x_i^T) u = u^T \left( \frac{1}{n-1} \sum_{i=1}^n x_i x_i^T \right) u $$
我们总结括号内的这样一大串东西为样本协方差矩阵 (Sample Covariance Matrix),记作 $S$。
$$ S = \frac{1}{n-1} X X^T $$
(注:这里假设 $X$ 是 $d \times n$,每列一个样本)
因此,我们得到了我们想要最大化的目标函数:
$$ \text{Maximize } \quad u^T S u $$
拉格朗日乘子法
如果我们只要求最大化 $u^T S u$,那简单了,把 $u$ 弄得无穷大就行了。但这没意义。我们要找的是方向。
所以必须限制 $u$ 是单位向量:
$$ \text{Subject to } \quad u^T u = 1 $$
为了解决带这样约束的优化问题,我们需要使用拉格朗日乘子法 (Lagrange Multipliers)。
我们引入拉格朗日函数 $\mathcal{L}$,$\lambda$ 是乘子:
$$ \mathcal{L}(u, \lambda) = u^T S u - \lambda (u^T u - 1) $$
对向量 $u$ 求偏导,并令其为 0:
- $u^T S u$ 对 $u$ 求导是 $2Su$(因为 $S$ 是对称阵,参考上一章 Ridge 的推导)。
- $u^T u$ 对 $u$ 求导是 $2u$。
可得:
$$ \frac{\partial \mathcal{L}}{\partial u} = 2Su - 2\lambda u = 0 $$
消去 2,移项,我们看到了那个熟悉的公式:
$$ \mathbf{S u = \lambda u} $$
这说明了什么?
- $u$ 必须是 $S$ 的特征向量
我们要找的那个“最优投影方向”,竟然就是协方差矩阵的特征向量。 - 方差到底有多大?
把 $Su = \lambda u$ 代回方差公式 $u^T S u$:
$$ \text{Var} = u^T (S u) = u^T (\lambda u) = \lambda (u^T u) = \lambda \cdot 1 = \lambda $$
你发现投影后的方差,正好等于对应的特征值 $\lambda$
到这里PCA就闭环了。我们的逻辑是:
算$S$ $\rightarrow$ 算$\lambda$和$u$ $\rightarrow$ 挑大的$\lambda$对应的$u$进行投影。
为了让方差最大 $\to$ 就要让 $\lambda$ 最大。所以:第一主成分 (PC1) = 最大特征值 $\lambda_1$ 对应的特征向量 $u_1$。
同理,第二主成分 (PC2) = 第二大特征值 $\lambda_2$ 对应的特征向量 $u_2$。以此类推。
我们来做一个思考题来更深入理解我们干了什么。如果数据$X$是二维的,均值为0。我们知道$S$是一个$2 \times 2$方阵。
如果
$$ S = \begin{bmatrix} 10 & 0 \\ 0 & 1 \end{bmatrix} $$
a) 这意味着这两个特征之间是相关的还是无关的?数据的分布形状大概是什么样子的?
b) 我们可以知道$S$的特征值分别是10和1,对应的特征向量就是$u_1 = [1, 0]^T$和$u_2 = [0, 1]^T$。 如果我们做PCA降维到1D,我们会选择哪个方向?保留下来的方差是多少?丢掉的信息量是多少?
c) 我们为什么要加上$u^Tu = 1$这个约束?直接最大化$u^TSu$结果会是什么样?
a):
我们之前推导出 $S = \frac{1}{n-1} XX^T$。这个矩阵是 PCA 的“地图”。它告诉我们数据的地形。
假设我们有 2 维数据 $(x_1, x_2)$。$S$ 是一个 $2 \times 2$ 矩阵:
$$ S = \begin{bmatrix} \text{Var}(x_1) & \text{Cov}(x_1, x_2) \\ \text{Cov}(x_2, x_1) & \text{Var}(x_2) \end{bmatrix} $$
则:
- 对角线元素 (Diagonal): $\text{Var}(x_1)$ 和 $\text{Var}(x_2)$。
- 这代表数据在轴向上的拉伸程度。数值越大,数据在这个轴上铺得越开。
- 非对角线元素 (Off-diagonal): $\text{Cov}(x_1, x_2)$。
- 这代表两个特征的联动程度。
- 如果是 0:说明 $x_1$ 变大时,$x_2$ 毫无规律(爱变不变)。这叫不相关 (Uncorrelated)。
- 如果是正数:说明 $x_1$ 变大,$x_2$ 也倾向于变大。数据分布会像一个向右上倾斜的雪茄。
回到这个问题,我们就可以通过$S$解读数据:
$$ S = \begin{bmatrix} 10 & 0 \\ 0 & 1 \end{bmatrix} $$
由于非对角线是 0 $\to$ 无相关性。
同时由于$x_1$ 方差是 10,$x_2$ 方差是 1。数据看起来就像一根沿着 X 轴平放的法棍面包。它在 X 轴很长(10),在 Y 轴很窄(1)。
b):
首先,特征值$\lambda$意味着什么?我们刚才推导出投影后的方差 = $\lambda$,在PCA中,方差=信息量,也就是说,如果所有数据都是一样的,方差为 0,没有任何信息;方差越大,区别度越高,信息越多。
回到问题,刚才的法棍面包矩阵得出的特征值分别是$\lambda_1 = 10$, $\lambda_2 = 1$,则我们可以得出:
- $\lambda_1 = 10$对应X轴方向的$u_1 = [1, 0]^T$。这根轴保留了10个单位的信息量。
- $\lambda_2 = 1$对应Y轴方向$u_2 = [0, 1]^T$。这跟轴只保留了1个单位的信息量。
那么如果我们要降维,我们肯定要保留$\lambda$最大的那个!因此,我们保留X轴,丢弃Y轴。
这样我们就保留了$\frac{10}{(10+1)} \approx 0.91$的原始信息,丢掉了百分之9的信息。
所以,特征值$\lambda$就是每个主成分的含金量,而PCA要做的就是按照含金量从高到低来淘金。
c):
由于PCA的目标是找一个“最佳拍摄角度”,如果我们不加$u^Tu = 1$的约束,直接最大化$u^TSu$,算法就会跑偏:
想象一下,我选定了一个最好的角度,打比方说X轴,此时$u = [1,0]^T$,方差=10。既然没有约束,那算法可能会“走神”,与其寻找一个最佳方向,算法也同时去拉长$u$的长度。最大化$u^TSu$会导致解趋向于无穷大,如果这样优化问题就是去意义了。
最小重构误差
我们知道PCA的目标是最大化投影方差,让数据分的越开越好。但同时我们也需要保证我们能最小化重构误差,也就是让丢掉的信息越少越好。它们之间有什么联系吗?
想象一下我们有一个数据点$x$,我们想要将其投影到直线$u$上。
你应该还记得啥是勾股定理吧?如果我们将:
- 斜边定义为原始向量$x$的长度 $a$
- 直角边1定义为投影向量的长度,也就是我们想要最大化的方差 $b$
- 直角边2定义为数据点到直线的垂直距离,那么这个就是我们想要最小化的损失 $c$
根据勾股定理,我们就知道
$$a^2 = b^2 + c^2$$
由于$a$是固定的,所以我们可以得出最大化投影长度就在同样最小化误差长度。
因此,PCA找到的那根轴,不仅是数据分布最广的方向,也是里所有数据点平均距离最近的那条线。这就是为什么我们可以用PCA来做压缩,因为它丢掉的信息最少。
奇异值分解 (SVD)
在之前的推导中,要是想做PCA,我们需要先算出协方差矩阵$S$,然后求$S$的特征值。但是有趣的是在实际工程中,我们几乎从不这么做,相反,我们直接对数据矩阵$X$做奇异值分解 (Singular Value Decomposition, SVD)。
什么是SVD?线性代数告诉我们,任何一个矩阵$X(d \times n)$都可以拆解成三个矩阵的乘积:
$$ X = U \Sigma V^T $$
- $U$: 左奇异向量 ($d \times d$, 正交阵)。
- $\Sigma$: 奇异值矩阵 ($d \times n$, 对角阵)。对角线上的 $\sigma_i$ 是 奇异值 (Singular Values)。
- $V$: 右奇异向量 ($n \times n$, 正交阵)。
让我们把 $X = U \Sigma V^T$ 代入协方差矩阵 $S$ 的公式看看会发生什么:
$$ S = \frac{1}{n-1} X X^T $$
$$ S = \frac{1}{n-1} (U \Sigma V^T) (U \Sigma V^T)^T $$
$$ S = \frac{1}{n-1} U \Sigma \underbrace{V^T V}_{=I} \Sigma^T U^T $$
$$ S = U \left( \frac{\Sigma \Sigma^T}{n-1} \right) U^T $$
回顾特征分解公式 $S = U \Lambda U^T$,对比上面两个式子,你会发现:
- PCA 的特征向量 (Eigenvectors) 正好就是 SVD 的左奇异向量 $U$
- PCA 的特征值 (Eigenvalues) $\lambda_i$ 与 SVD 的奇异值 $\sigma_i$ 存在换算关系:
$$ \lambda_i = \frac{\sigma_i^2}{n-1} $$
那么说得好,我们为什么会使用SVD呢?SVD好在哪?计算 $XX^T$ 会导致数字精度损失(平方会让很小的数变得极小,很大的数变得极大)。SVD 直接在 $X$ 上操作,数值更稳定,而且现代SVD算法更加高效。
本章小结
这一章我们攻克了无监督学习的第二座堡垒——降维。
- 我们发现 降维 = 找一个投影方向,让数据投影后的方差最大,保留最多信息。
- 数学结论:这个"最佳方向"竟然就是协方差矩阵$S$的最大特征向量。
- 操作流程:中心化数据 → 算协方差矩阵$S$ → 算特征值和特征向量 → 选最大的几个投影。
- 聚类 (Ch7):在样本之间找关系(把相似的样本归为一类)。
- PCA (Ch8):在特征之间找关系(把相关的特征合并成主成分)。
至此,我们已经翻越了"第二座山"。我们学会了在有标签时怎么预测(监督学习),在没标签时怎么找结构(无监督学习)。
但这些模型都是"静态"的——给一个输入,吐一个输出,结束。
如果你的模型是一个机器人,它做出的动作会改变环境,环境又会反过来影响它,这该怎么学?